一列简谐波沿x轴正向传播,在t1=0s,t1=0.25s时刻的波形如图所示.试求: (1)P点的振动表达式; (2)波动方程; (3)画出O点的振动曲线. 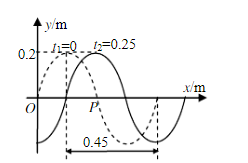
正确答案:
(1)设P点的振动方程为yP=Acos(ωt+θ),其中A=0.2m.
在Δt=0.25s内,波向右传播了Δx=0.45/3=0.15(m),所以波速为u=Δx/Δt=0.6(m·s-1).
波长为:λ=4Δx=0.6(m),周期为:T=λ/u=1(s),圆频率为:ω=2π/T=2π.
当t=0时,yP=0,因此cosθ=0;
由于波沿x轴正向传播,所以P点在此时向上运动,速度大于零,所以θ=-π/2.
P点的振动表达式为:yP=0.2cos(2πt-π/2).
在Δt=0.25s内,波向右传播了Δx=0.45/3=0.15(m),所以波速为u=Δx/Δt=0.6(m·s-1).
波长为:λ=4Δx=0.6(m),周期为:T=λ/u=1(s),圆频率为:ω=2π/T=2π.
当t=0时,yP=0,因此cosθ=0;
由于波沿x轴正向传播,所以P点在此时向上运动,速度大于零,所以θ=-π/2.
P点的振动表达式为:yP=0.2cos(2πt-π/2).

答案解析:有

微信扫一扫手机做题
