试证明:一个BCNF范式必是3NF。
正确答案:
用反证法。
设R是一个BCNF,但不是3NF。
则必存在非主属性A和候选关键字X以及属性集Y,使得X→Y,Y→A,其中A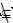 X,A
X,A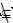 Y,Y X∈F+,这就是说Y不可能包含R的关键字,但Y→A却成立。
Y,Y X∈F+,这就是说Y不可能包含R的关键字,但Y→A却成立。
根据BCNF定义,R不是BCNF,与题设矛盾,所以一个BCNF范式是3NF。
设R是一个BCNF,但不是3NF。
则必存在非主属性A和候选关键字X以及属性集Y,使得X→Y,Y→A,其中A
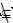 X,A
X,A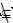 Y,Y X∈F+,这就是说Y不可能包含R的关键字,但Y→A却成立。
Y,Y X∈F+,这就是说Y不可能包含R的关键字,但Y→A却成立。 根据BCNF定义,R不是BCNF,与题设矛盾,所以一个BCNF范式是3NF。
答案解析:有

微信扫一扫手机做题
