设G＝（V，E）是一个赋权有向图，其顶点集V被划分成k>2个不相交的子集V_i：1≤i≤k，其中，V₁和V_k分别只有一个顶点s（称为源）和一个顶点t（称为汇），图中所有的边（u，v），u∈V_i，v∈V_i+1。求由s到t的最小成本路径。 a）给出使用动态规划算法求解多段图问题的基本思想。 b）使用上述方法求解如下多段图问题。

正确答案:（1）基本思想：设P（i，j）是从Vi中的节点j到汇点t的最小成本路径，Cost（i，j）是其成本。则Cost（i，j）=min{c（j，h）+Cost（i+1，h）
H.V_i+1，（j，h）∈E}。
边界条件是若h=t，则Cost（h，t）＝0；Cost（k-1，j）＝c（j，t）。
（2）求解过程可以表示为：

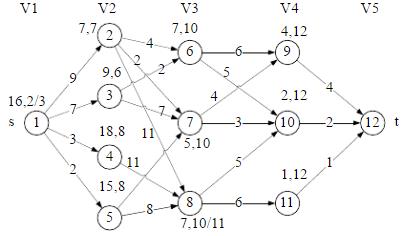
其中每个节点标示的序偶（p，q）中，p表示节点到t的成本，q表示后继节点的编号。
从而，最优路径为：1→2→7→10→12和1→3→6→10→12，成本为16。